Burrows Wheeler Transform と Suffix Array 

　　　　　　　　 ,. -‐'''''""¨¨¨ヽ 
　　　　 　 　 (.＿＿_,,,... -ｧァﾌ|　　　　　　　　　　あ…ありのまま 今日　起こった事を話すぜ！ 
　 　 　 　 　 |i i|　 　 }!　}} /／| 
　　　　 　 　 |l､{　 　j}　/,,ｨ//｜　　　　　　　『BWT について調べていたら Suffix Array のライブラリができていた』 
　　　　　　　 i|:!ヾ､_ﾉ／ u {:}//ﾍ　　　　　　　　　　　 
　　　　　　　 |ﾘ u' }　 ,ﾉ　_,!V,ﾊ |　　 
　　 　 　 ／´fト､_{ﾙ{,ィ'ｅﾗ　, ﾀ人　　　　　　　　な…　何を言ってるのか　わからねーと思うが 
　　　　 /' 　 ヾ|宀| {´,)⌒`/ |<ヽﾄiゝ　　　　　　　　おれも何をされたのかわからなかった… 
　　　　,ﾞ　 ／ )ヽ iLﾚ 　u' |　| ヾｌﾄﾊ〉 
　　 　 |／_／　 ﾊ !ニ⊇　'／:} 　V:::::ヽ　　　　　　　　頭がどうにかなりそうだった… 
　　　 /／ 二二二7'T'' ／u'　__ /:::::::/｀ヽ 
　　　/'´r　-―一ｧ‐ﾞＴ´　'"´ ／::::／-‐ 　＼　　　　　 組み込みの sort関数とかマルチキークイックソートとか 
　　 / // 　 广¨´ 　/'　　 ／:::::／´￣｀ヽ ⌒ヽ　　　　　そんなチャチなもんじゃあ　断じてねえ 
　　ﾉ ' /　 ノ:::::`ー-､___／:::::／/ 　 　 　 ヽ　　}　　　　　 　 
_／｀丶　/::::::::::::::::::::::::::￣`ー-{:::...　　　 　　　ｲ　 　　もっと恐ろしい、「libdivsufsort」の速度を味わったぜ…


... ということで libdivsufsort の Perl バインディング Algorithm::DivSufSort を以下に置いておきます。*1

Burrows Wheeler Transform の簡単な解説

Burrows Wheeler Transform (または Block Sorting、以下 BWT もしくはブロックソーティング) は、テキストの可逆変換のアルゴリズムで広くは bzip2 の圧縮などに利用されています。BWT で変換したテキストそのものは元テキストとサイズは変わりませんが、圧縮しやすい状態になります。

試しに、Lorem ipsum - Wikipedia にある

[32] Sed ut perspiciatis, unde omnis iste natus error sit voluptatem accusantium doloremque laudantium, totam rem aperiam eaque ipsa, quae ab illo inventore veritatis et quasi architecto beatae vitae dicta sunt, explicabo...

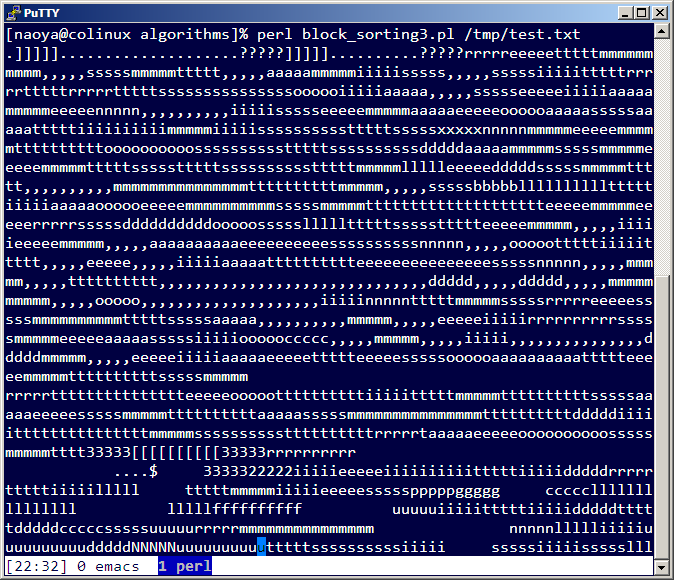
というテキストを数回続けたテキストを用意して BWT で変換した出力は以下のようになりました。スクリーンショットを載せておきます。

同じような記号がずらずらと並んでいるのが分かります。このように同じ記号が長く続くデータは圧縮に有利です。この BWT 後のテキストに先頭移動法を施して更に圧縮しやすい形に変換した後、ハフマン符号や算術符号でエントロピー符号化するのが定番です。

BWT が面白いのは、このずらずらと並んだテキストから元のテキストを復元することができるところです。以下 BWT アルゴリズムの簡単な説明です。

abracadabra という文字列があるとします。これを変換します。

  • 末尾が分かるように $ を追加します → abracadabra$
  • abracadabra$ の先頭の文字 a を末尾に移動させると bracadabra$a になります
  • bracadabra$a の先頭の文字 b を末尾に移動させると racadabra$ab になります

これを繰り返すと以下のような「ブロック」が得られます。

abracadabra$
bracadabra$a
racadabra$ab
acadabra$abr
cadabra$abra
adabra$abrac
dabra$abraca
abra$abracad
bra$abracada
ra$abracadab
a$abracadabr
$abracadabra

このブロックの行を辞書式順にソートします。

$abracadabra
a$abracadabr
abra$abracad
abracadabra$
acadabra$abr
adabra$abrac
bra$abracada
bracadabra$a
cadabra$abra
dabra$abraca
ra$abracadab
racadabra$ab

となります。このソート済みブロックの各行の末尾から一文字ずつ取ると ard$rcaaaabb という文字列 (これを L とします) が得られます。これが変換済み文字列です。a が連続して出現していることが分かります。先頭の文字を末尾に持ってきてソートしただけなので、この変換済み文字列にはオリジナルの文字列で出現するすべての文字列が含まれているところがポイントです。

次は逆変換のアルゴリズムです。L を辞書式順にソートしてみます。

L    F
------
a    $ 
r    a
d    a
$    a
r    a
c    a
a    b
a    b
a    c
a    d
b    r
b    r

すると、先のブロックの先頭の列 $aaaaabbcdrr (これを F とします) が得られました。元々末尾の文字は先頭の文字を持ってきたものなので、ソートするとブロックの先頭が得られるのは当然です。

L、F の文字の対応行をそれぞれ見てみます。 a$ ... ra ... da ... $a ... ra ... ca ... ab ... ab ... ac ... ad ... br じっくり見てみると全てのペアは abracadabra$ の中の一部分になっていることが分かります。

  • a$ は abracadabr"a$"
  • ra は ab"ra"cadab"ra"$　のいずれか
  • da は abraca"da"bra$
  • ...

などです。この二文字を適当な順番で繋げていくと元テキストが復元できそうです。

話は変わって、L をどう作ったかを思い出します。先頭の文字 F を順番に末尾 L に持ってきたのでした。「L は常に F のひとつ前」の文字を指していることになります。

L      F
---------
a0    $ 
r     a0
d     a1
$     a2
r     a3
c     a4
a1    b0
a2    b1
a3    c
a4    d
b0    r
b1    r

F の中から、まずオリジナルの文字列の abracadabra の先頭の 'a' がどれだったかを探してみます。複数出現する文字は分かりやすいように数値を付与しておきます。「L は常に F のひとつ前」です。先頭 a のひとつ前...ということは何もないわけですが、ブロックは回転して作っているので末尾を指す $ になります。L が $ の行は F は a2 です。

  • この F = a2 が "abracadabra" のはじまりの a です。
  • 次に L の a2 の行に着目します。a2 と繋がっているのは F = b1 です
  • L = b1 のとき F = r
  • L = r のとき F = a3
  • L = a3 のとき F = c
  • L = c のとき F = a4
  • ...

と L = $ (L[3]) から出発して L → F → L → F と繋げていくと F[] から "abracadabra$" が出てきました。

このように

  • 先頭文字を末尾に順番に移動したブロックをソートして得られたブロックの末尾の文字を出力するのが BW 変換 (= ブロックソーティング)
  • BWT 変換された文字列をソートして L と F を作り、文字の開始位置から LF マップを辿っていってオリジナルを求めるのが BW 逆変換

になります。

ブロックソーティングの実装

ブロックソーティングを、まずはコストを考えずに Perl で実装したものが以下のコードです。

まずはエンコード。入力はかならず最後に "$" がついていることを前提にしたコードです。

sub bs_encode ($) {
    my $text = shift;
    my $len = length $text;

    my @block;
    for (my $i = 0; $i < $len; $i++) {
        $block[$i] = $text;

        ## 末尾に先頭一文字を移動
        $text .= substr($text, 0, 1);
        substr($text, 0, 1) = '';
    }

    ## ソート済みのブロックの各行から末尾一文字を返す
    return join '', map { substr($_, -1, 1) } sort @block;
}

テキストを受け取って、ブロックを作ります。最後の行ではブロックを組み込みの sort () ソートして末尾一文字を substr() で取得して結合して返却しています。コストを考えなければ意外と簡単です。

次はデコードです。

sub bs_decode ($) {
    my $bwt = shift;

    my $len = length $bwt;
    my @data = split //, $bwt;

    ## 末尾のポジションを調べる
    my $pos = 0;
    for (; $pos < @data; $pos++) {
        if ($data[$pos] eq "\$") {
            last;
        }
    }

    ## F は文字で持つのではなくインデックスで持つ
    my @LFMapping = sort { $data[$a] cmp $data[$b] } (0..$len - 1);

    my @buf;
    for (my $i = 0; $i < $len; $i++) {
        $pos = $LFMapping[ $pos ];
        push @buf, $data[ $pos ];
    }

    return join '', @buf;
}

BW 変換済みのテキストを受け取って、まずは $ のインデックスを調べます。続けて L から F を求めます。最終的に必要になるのは F の文字ではなく F がどういう順番で並んでいるかという、位置情報 (インデックスです)。そこで LFMapping という配列に F 相当の並びのインデックスを作ります。あとは LFMapping を、先に求めた $ のインデックスから開始して辿っていくだけです。

bs_ecnode()、bs_decode() を実際に使ってみます。

#!/usr/local/bin/perl
use strict;
use warnings;
use Perl6::Say;

my $text = shift or die "usage: $0 <text>";

my $bwt = bs_encode $text;
say $bwt;
say bs_decode $bwt;

% perl block_sorting0.pl abracadabra$
ard$rcaaaabb
abracadabra$

という結果となりました。

デコードの改善

エンコード処理、デコード処理共にアルゴリズムの計算量/空間量的に改善できる余地が相当あります。エンコード処理の方が改善の余地が大きいので後回しにして、まずはデコードを改善してみます。

先のデコード処理では、まず $ の位置を探して、その後にソートを施しています。文字を探索するのに O(n)、LFMapping を作る際のソートに O(nlogn) のコストがかかっています。ここは分布数え上げソートを使って計算量を減らすことができます。(本質とは少し離れますが、関数の入出力を値渡しにするとテキストデータのコピーが発生するので実際には参照渡しで実装した方が良いでしょう。)

use constant UCHAR_MAX => 0x100;

sub bs_decode ($) {
    my $bwt = shift;

    my $len  = length $bwt;
    my @data = split //, $bwt;
    my $pos = - 1;

    ## 分布数え上げソート
    my @count;
    for (my $i = 0; $i < UCHAR_MAX; $i++) {
        $count[$i] = 0;
    }

    for (my $i = 0; $i < $len; $i++) {
        ## 分布数え上げソート中に $ をついでに探す
        if ($data[$i] eq "\$") {
            $pos = $i;
        }
        $count[ ord $data[$i] ]++;
    }

    for (my $i = 0; $i < UCHAR_MAX; $i++) {
        $count[$i] += $count[$i - 1];
    }

    my @LFmapping;
    for (my $i = $len - 1; $i >= 0; $i--) {
        $LFmapping[ --$count[ ord $data[$i] ] ] = $i;
    }

    my @buf;
    for (0..$len - 1) {
        $pos = $LFmapping[ $pos ];
        push @buf, $data[ $pos ];
    }

    return join '', @buf;
}

分布数え上げソートで記号の出現頻度を数える際、文字列を先頭から舐めることになります。このときに $ をついでに探します。分布数え上げソートのコストは O(n) なので計算量が改善されます。

エンコード処理の改善 その1

先の実装では、アルゴリズム的にエンコード処理で問題になるのは二点あります。

  • 空間のコスト。先の実装では文字の長さ N に対して、回転した文字列を N 個もつことになるので合計 N * N = N^2 バイトのメモリを使ってしまう
  • ソートのコスト

まずは空間コストを削減する良い方法は、文字をすべて持つのではなくインデックスで管理することです。よく知られている方法に abracadabra という入力があったら abracadabraabracadabra という同じ文字を繋げる方法があります。

  • "abracadabra"abracadabra
  • a"bracadabraa"bracadabra
  • ab"racadabraab"racadabra
  • abr"acadabraabr"acadabra

と固定幅でポイントをずらしていくと abracadabraabracadabra という 2N の長さの文字列から、ブロックソーティングに必要な文字列すべてが得られることがわかります。L個の各文字列は文字の開始位置つまりオフセットを覚えて置けばよいので、整数 4 バイト * N = 4N サイズになります。結局合計で 2N + 4N = 6N の空間でブロックソーティングが可能になります。

この方法で実装したブロックソーティングが以下です。ソートの計算量はまだ O(n^2logn) です。

sub bs_encode ($) {
    my $data = shift;

    my $len = length $data;
    my @datadata = split //, $data x 2; ## abracadabraabracadabra

    ## インデックスを @datadata を基準にソートする
    ## ここのソートは O(n^2 log n)、要改善
    my @index = sort {
        my $r;
        for (my $i = 0; $i < $size; $i++) {
            $r = $datadata[$a + $i] cmp $datadata[$b + $i];
            if ($r != 0) {
                return $r;
            }
        }
        return 0;
    } (0..$size -1);

    ## index はブロックの各行の開始位置なので index[i + len - 1] が末尾の文字
    my @buf;
    for (@index) {
        push @buf, $datadata[$_ + $len - 1];
    }

    return join '', @buf;
}

エンコード処理の改善その2

先の改善で空間消費量は 6N に抑えることができましたが、より改善する方法があります。ブロックソートの終了条件について考えます。

abracadabra$
bracadabra$a
racadabra$ab
acadabra$abr
cadabra$abra
adabra$abrac
dabra$abraca
abra$abracad
bra$abracada
ra$abracadab
a$abracadabr
$abracadabra

というブロックをソートするのに実際に必要な情報は $ を番兵とみなすとこのブロック全てではなく

abracadabra$
bracadabra$
racadabra$
acadabra$
cadabra$
adabra$
dabra$
abra$
bra$
ra$
a$
$

という情報だけで済みます。実際にこれをソートすると

$
a$
abra$
abracadabra$
acadabra$
adabra$
bra$
bracadabra$
cadabra$
dabra$
ra$
racadabra$

という結果になり、先頭はちゃんと F になっています。ただしこれだと最終的に知りたい L が分かりません。ここでアルゴリズムの解説の逆変換でも利用した「L は常に F のひとつ前」という性質を利用します。つまり F[i - 1] = L[i] です! (F[i] の i = 0 の場合は $ が来ます。)

結局、この手法を採用すると N + 1 に位置情報の 4(N + 1) を加えて 5N + 5 バイトでブロックソーティングが可能です。

以上を施したコードは以下になりました。

sub bs_encode ($) {
    my $data = shift;

    my @data = split //, $data;
    my @index = sort {
        my $r;
        for (my $i = 0; $i < @data; $i++) {
            $r = ord $data[$a + $i] <=> ord $data[$b + $i];

            if ($r != 0) {
                return $r;
            }
        }
        return 0;
    } (0.. @data - 1);

    ## $data[$i] はソート済みブロックの先頭文字 (LF Mapping の F)
    ## $data[$i - 1] は LFMapping の L
    ## Perl の配列は添え字 -1 の時は末尾を指すのを利用
    my @buf;
    for my $i (@index) {
        push @buf, $data[$i - 1];
    }

    return join '', @buf;
}

BWT と Suffix Array

ようやく今回の本題です。先にブロックソートしたデータを見てみましょう。

$
a$
abra$
abracadabra$
acadabra$
adabra$
bra$
bracadabra$
cadabra$
dabra$
ra$
racadabra$

というデータです。そして F[-1] = L を利用するときに必要なのは F のインデックス値、つまりこのデータの先頭のインデックスでした。どこかで見たことがある形です。これは Suffix Array (接尾辞配列) です! Suffix Array があれば、そこから BWT 後のテキストが得られます。

Suffix Array を SA[0..n]、BW変換後のテキストを BWT[0..n]、入力文字列を T[0..n] とすると、

  • BWT[i] = T[SA[i] -1]

です。

高速な Suffix ソーティング

先のアルゴリズムではソートの計算量がまだ改善されていませんでした。そこでソートを改善するのですが、ブロックソーティングの問題は Suffix Array を得ることに等しいのでした。Suffix Array を効率的に求めるアルゴリズムは多数知られています。また 2008 年の現在でも新たなアルゴリズムが提案されています。

bzip2 でも使われている、始めに先頭二文字で基数ソートをして途中からソートアルゴリズムを切り替える方法 (MSD Radix Sort の改良版のようなもの) から、より高度な Larsson Sadakane 法や二段階ソート法など様々なものがあります ... すいません、まだ高度な方法はまだ理解が曖昧なので解説は今度にします。

これらのアルゴリズムのうち効率的なものを選んで実装すれば、より高速にブロックソーティングが可能になります。

libdivsufsort

高速な Suffix Array 構築ライブラリに libdivsufsort があります。libdivsufsort は README によると

libdivsufsort uses the following algorithms for suffix sorting.

  • The improved version of Itho-Tanaka two-stage sorting algorithm. [2][6]
  • A substring sorting/encoding technique. [1][3]
  • Maniscalco's tandem repeat sorting algorithm. [5]
  • Larsson-Sadakane sorting algorithm. [4]

とのことで、二段階ソート法やLarsson Sadakane 法をベースに実装されていて、5N バイトを使用し最悪ケースで O(nlogn) でソートします。(README 内に各手法の論文への参照があります。) この辺も後日調べてまとめてみたいと思います。

Algorithm::DivSufSort

divsufsort() 関数を Perl でも利用したい、ということで libdivsufsort の Perl バインディングである Algorithm::DivSufSort を作りました...というのが冒頭の話です。随分遠回りしました。

libdivsufsort には高速な Suffix ソーティングである divsufsort() 関数以外にも BWT 用の関数も実装されていますが、今のところは divsufsort() のグルーのみの実装となります。

my $sa = divsufsort("abracadabra");

これだけで高速に Suffix Array が構築できます。戻り値は配列リファレンスです。

Algorthm::DivSufSort の改善点

Algorithm::DivSufSort は XS ですが

int
_divsufsort(SV *src, AV *sa, int size) {
    int st, i;
    saidx_t *SA;

    SA = malloc(size * sizeof(saidx_t));
    st = divsufsort(SvPV(src, size), SA, size);
    av_extend(sa, size);

    for (i = 0; i < size; i++) {
        // fprintf(stderr, "sa[%d] = %d\n", i, SA[i]);
        av_store(sa, i, newSViv(SA[i]));
    }

    free(SA);

    return st;
}

という実装になっています。divsufsort() に渡す用の saidx_t SA が Suffix Array です。この divsufsort() から構築された SA を、Perl の配列の構造である AV に定数時間で変換することができればより良いのですが、今はやり方がわからず先頭からコピーしてしまっています。ここは改善できるなら改善したいところです。

Algorithm::DivSufSort を使ってブロックソーティング

divsufsort を使って Suffix Array を構築し、そこから BWT 文字列を得るよう、bs_encode() を実装してみます。

sub bs_encode ($) {
    my $text = shift;

    my $sa = divsufsort($text);

    my @text = split //, $text;
    my @buf;
    for my $i (@$sa) {
        push @buf, $text[$i - 1];
    }

    return join '', @buf;
}

一番難しい Suffix Array の構築は divsufsort() がやってくれます。これはもう少し短く書くことができて

sub bs_encode ($) {
    my $text = shift;
    my @text = split //, $text;
    return join '', map { $text[$_ - 1] } @{ divsufsort($text) };
}

となりました。

なお、libdivsufsort はBWT用の関数も提供しています。ここでは Suffix Array → BWT の変換過程を見るために敢えて divsufsort() のみ利用しています。

CSA と FM-index

Suffix Array があれば BWT 文字列が得られることが分かりました。この両者の関係も面白いのですが、より面白いのは Compressed Suffix Array (圧縮接尾辞配列) と FM-index の関係です。

CSA は、Suffix Array をある規則に従って変換して圧縮しやすい形にしたデータ構造で圧縮全文検索索引を実現します。一方、FM-index は BWT 後のテキストに rank(), select() 操作を適用することで圧縮全文検索索引を実現します。それぞれ別方向から圧縮全文索引を実現していますが、両者は逆マッピングの関係にあるそうです。

この辺りについても理解が進んだところでまた言及してみたいと思います。

まとめ

  • libdivsufsort の Perl バインディングである Algorithm::DivSufSort を作りました
  • Burrows Wheeler Transform と Suffix Array は BWT[i] = T[SA[i] - 1] の関係にあります
  • Suffix Array が構築できれば、ほんのちょっとの追加処理で BWT 文字列が得られます
  • Suffix Array を効率的高速に構築する手法は多数知られています
  • CSA の実装や FM-index の関係についてももう少し調べて後日まとめてみたいと思います
  • Algorithm::DivSufSort 利用と他の実装でのベンチマークも後日掲載します

参考文献

*1:まだ divsufsort() のみしかサポートしていません