Latent Semantic Indexing - naoyaのはてなダイアリー

情報検索におけるベクトル空間モデルでは、文書をベクトルとみなして線形空間でそれを扱います。この文書ベクトルは、文書に含まれる単語の出現頻度などを成分に取ります。結果、以下のような単語文書行列 (term document matrix) が得られます。

	d₁	d₂	d₄
Apple	3	0	0
Linux	0	1	1
MacOSX	2	0	0
Perl	0	1	0
Ruby	0	1	3

この単語文書行列に対して内積による類似度などの計算を行って、情報要求に適合する文書を探すのがベクトル空間モデルによる検索モデルです。

見ての通り、単語文書行列の次元数は索引語の総数です。文書が増えれば増えるほど次元は増加する傾向にあります。例えば索引語が100万語あって検索対象の文書が 1,000万件あると、100万次元 * 1,000万という大きさの行列を扱うことになりますが、単語文書行列がスパースであることをうまく利用すことで計算量を現実的な量に抑えこむことができます。転置インデックスのデータ構造はスパースな単語文書行列を処理するの適しています。

スパースであることを利用して計算量を下げるという方法以外に、単語文書行列をより小さな行列で近似することで計算量を下げようという手法があります。

ところで、単語文書行列を用いた情報検索での大きな欠点は、類似語あるいは同義語も別次元として扱われてしまう点です。"car" という検索質問に対しては "automobile" を含む文書も検索したいところですがそれぞれの索引語は別次元なのでうまくいきません。

Latent Semantic Indexing (LSI, 潜在的意味インデキシング) は、高次元の空間にある単語文書行列を射影により小さな行列で近似し検索精度の改善を図る技術です。近似にあたっては行列の特異値分解 (Singular value decomposition, SVD) を使って、相互に関連のありそうな索引語の次元を特定の次元に縮退させることで全体の次元を削減するという方針を採ります。これにより行列計算の計算量を下げつつ検索精度を向上させることができるという一挙両得の手法です。

Introduction to Information Retrieval の 18 章のテーマがこの LSI でした。情報検索アルゴリズムでも解説されています。両著を読んでの感想・考察を以下に記します。

IIR 18章における固有値の直感的イメージ

LSI では線型代数の演算、特に固有値を利用した行列演算を多用します。特異値分解の解説の前段として IIR、情報検索アルゴリズム両著で行列の固有値分解について触れられています。それぞれ異なる視点での解説となっていますが、ここで両者の視点を繋げてみたいと思います。

IIR では、固有ベクトルの線形結合の計算結果から、固有値が与える次元の重みについて論じています。

例として、以下の対称行列 S を考えます。

$S = \begin{pmatrix} 30&0&0 \\0&20&0 \\0&0&1 \end{pmatrix}$

この行列の固有値は λ₁ = 30, λ₂ = 20, λ₃ = 1 となります。それぞれの固有値に対応する固有ベクトルとして

$\vec{x_\1} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$ , $\vec{x_\2} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$ , $\vec{x_\3} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$

を選びます。異なる固有値に対する固有ベクトルは必ず一次独立なので、この3本の固有ベクトルの線形結合で任意の3次元ベクトルを表現することができます。

例えば

$\vec{v} = \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}$

というベクトルは

$\vec{v} = \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix} = 2\vec{x_\1} + 4\vec{x_\2} + 6\vec{x_\3}$

という線形結合で表現されます。

このベクトル $\vec{v}$ に対して行列 S を乗算してみます。

$\begin{eqnarray} S\vec{v} &=& S$2\vec{x_\1} + 4\vec{x_\2} + 6\vec{x_\3}$ \\&=& 2S\vec{x_\1} + 4S\vec{x_\2} + 6S\vec{x_\3} \\&=& 2\lambda_\1\vec{x_\1} + 4\lambda_\2\vec{x_\2} + 6\lambda_\3\vec{x_\3} \\&=& 60\vec{x_\1} + 80\vec{x_\2} + 6\vec{x_\3} \end{eqnarray}$

という結果になりました。

さて、この数式から以下のことがわかりります。IIR 18章から引用します。(日本語部分は id:sleepy_yoshi さんによる和訳から)

Example 18.1 shows that even though $\vec{v}$ is an arbitrary vector, the effect of multiplication by S is determined by the eigenvalues and eigenvectors of S. Furthermore, it is intuitively apparent from Equation (18.3) that the product $S\vec{v}$ is relatively unaffected by terms arising from the small eigenvalues of S.
例 18.1 は、 $\vec{v}$ が任意のベクトルであっても、S による乗算の効果は S の固有ベクトルと固有値によって決定されるということを示している。更に、 $S\vec{v}$ の積が S の小さい固有値によって相対的に影響されにくいことが式 (18.3) より直感的に理解できる。

式 (18.3) というのは、引用直前の数式のことです。要するに、固有値が他と比べて相対的に小さいベクトルは、固有ベクトルによる線形結合において支配的でない、ということを述べています。

これが IIR 18章が挙げている例です。 $S\vec{v}$ という行列ベクトル積は、S による $\vec{v}$ の一次変換です。つまり、 $\vec{v}$ に S による一次変換を施すにあたって、 $\vec{v}$ を S の固有ベクトルの線形結合で表現しておくと、S による一次変換においてどの固有ベクトル成分が、変換後のベクトルにおいて支配的かが分かるというわけです。

繰り返しになりますが、これは固有ベクトルの張る線形空間において、小さな固有値とそれに対応する固有ベクトルの影響が小さいことを表しています。例えば $\vec{v}$ からλ₃ = 1 の固有ベクトルを完全に無視すると $S\vec{v}$ で得られるベクトルは (60, 80, 6)^T ではなく (60, 80, 0)^T となりますが、この二つのベクトルは λ³ = 1 の固有ベクトルの次元を無視したにも関わらず(コサイン類似度などでも)比較的近いベクトルであることがわかります。

IIR 18章では固有値と次元の削減の関係について、このような直感的イメージを与えています。

情報検索アルゴリズム 4.4.1 における主成分分析の解説

IIR の説明はわかりやすいのですが、あくまで直感的イメージです。情報検索アルゴリズムの 4.4.1 では同様の話題を主成分分析を例にもう少し厳密に解説しています。

基底の変換により主軸を見つける

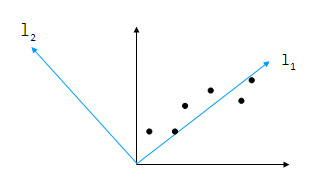
P.67 の図同様の図を作図してみました。

2次元空間上に幾つかのデータ (黒点) が分布しています。この2次元データを、2次元ではなく1次元のデータに変換したいとします。ここで線形変換により座標系を黒い2本の軸から、水色の2本に変換します。するとデータは l₁ 側に集中しますから、l₂ の次元を無視してしまってもその影響を小さく留めることができます。IIR 18章で固有値の小さな次元を無視した例と良く似ています。

うまく座標系を変換することで無視すべき方向が得られるのですが、ではどのような変換を施すべきでしょうか。特定の次元を無視したときに、なるべく情報量を損なわないような基底を求めるべきです。情報量を損なわない = 情報量を最大にすることであり、それはデータの分散が大きくなるような基底を求めることに等しい。そこで共分散行列 (covariance matrix) の固有ベクトルを利用するのが主成分分析です。

なぜ共分散行列の固有ベクトルを用いるのが良いかを書籍から引用しながら、見ていきます。

m 個の変量を持つ多次元データを以下の行列で表現します。行列の各行が1つのデータを表し行方向に各データの持つ変量値が記述される行列です。

$D = \begin{bmatrix} d_{\1\1}&d_{\1\2}&\cdots&d_{\1n} \\d_{\2\1}&d_{\2\2}&\cdots& d_{\2n} \\\vdots&\vdots&\ddots&\vdots \\d_{m\1}&d_{m\2}&\cdots&d_{mn} \end{bmatrix}$

データ行列 D に対し、i 番目の変量の平均をμ_iとします。

$\m_{i} = \frac1{n}\sum_{k=1}^{n}d_{ik}$

このデータを元にした共分散行列 S を考えます。

$S = \begin{bmatrix} s_{\1\1}&s_{\1\2}&\cdots&d_{\1n} \\s_{\2\1}&s_{\2\2}&\cdots& d_{\2n} \\\vdots&\vdots&\ddots&\vdots \\s_{m\1}&s_{m\2}&\cdots&s_{mn} \end{bmatrix}$

ただし

$s_{ij} = \frac1{n}\sum_{k=1}^{n}(d_{ik} - \m_{i})(d_{jk} - \m_{j})$

です。共分散行列は各対角要素が分散、非対角要素が共分散となります。この性質が固有値、固有ベクトルと相性が良いというのはなんとなく想像が付くでしょう。

ここで同じ共分散行列を別の方向から作ってみます。平均 μ_i を i 行目の要素に持つ m x n 行列 M を

$M = \begin{bmatrix} \m_{\1}&\m_{\1}&\cdots&\m_{\1} \\\m_{\2}&\m_{\2}&\cdots& \m_{\2} \\\vdots&\vdots&\ddots&\vdots \\\m_{m}&\m_{m}&\cdots&\m_{m} \end{bmatrix}$

とすると S は

$S = \frac1{n}(D - M)(D - M)^{T}$

とも表現されます。

これは行列 (D - M) の自己相関行列 (autocorrelation matrix) です。A = D - M とすると AA^T なので、S は対称行列です。よって固有値分解が使えます。S を固有値分解した結果は

$S = U{\Lambda}U^{T}$

となります。U は S の固有ベクトルによって構成される行列ですが、主成分分析においてこの固有ベクトルは主成分と呼ばれます。ここでそもそもの分析対象だった m 次元データ d を、この主成分を基底とする座標系に変換してみます。

$d^{\prime} = U^{T}d$

となります。この基底変換後のデータで共分散行列 $S^{\prime}$ を作ると

$S^{\prime} = U^{T}SU = {\Lambda}$

となります。(ちなみに、分解対称の行列 S は対称行列で、対称行列から得られる固有ベクトルはお互いに直交します。よって U は直交系であり、正規化することで正規直交系となります。)

さて、Λ は固有値分解によって得られた対角行列ですから、この対角要素は固有値です。また非対角要素は 0 です。すなわち、主成分を基底とする座標系では、各変量の分散が元のデータの共分散行列Sの固有値に等しく、しかも各変量間の共分散が 0 (無相関) になることが分かります。

まとめると

共分散行列 S を考える
S の固有値が大きいものを選んで対応する固有ベクトル(主成分)を得る
この固有値が大きい主成分を選ぶという過程が、分散が大きい軸を選んでいることに等しい
元データを、選ばれた主成分を基底とする座標系に変換する

という流れで、重要な次元だけを残して次元を削減できるということが分かります。固有値が主成分の重みを与えるということで、これは先に見た IIR 18章の直感的な説明と結びつきます。また、主成分分析と特異値分解との関連でいくと「データを表現するための最適な基底として自己相関行列の固有ベクトルを求めた」というところがポイントになります。

行列の特異値分解 (Singular value decompositions, SVD)

行列の固有値分解は正方行列を対称にしています。しかし M x N 単語文書行列は多くの場合正方でも、対称でもない M ≠ N の行列です。特異値分解を使うと　M x N 単語文書を分解することができますが、主成分分析で固有値が主成分の重みを与えたのと同様に、特異値分解では固有値の平方根である特異値という値が、基底に重みを与えます。この重みを考慮しながら行列の階数を削減していくことで、低階数近似による次元削減が可能です。

特異値分解においては、M ≠ N 行列 D そのままでは分解が難しいので、 DD^T と D^TD という D に対して定義できる二つの自己相関行列を利用します。自己相関行列は必ず対称行列になるので、固有値による操作が容易になります。結果、特異値分解により以下の式を得ます。

$D = U{\Sigma}V^T$

ここで

U は DD^T の固有ベクトルを列とする行列 (DD^T は対称行列であるため、U は直交行列)
V は D^TD の固有ベクトルを列とする行列 (D^TD は対称行列であるため、V は直交行列)

です。

U は左特異行列、V は右特異行列と呼ばれる
面白い性質として、DD^T と D^TD の固有値が等しい
Σは固有値分解における固有値を対角要素に持つ行列と良く似た形をしていて、その対角要素はこの固有値の平方根 σ_ij = (λ_ij)^1/2 となっている。σ を特異値と呼ぶ

この式は、自己相関行列の固有ベクトルを基底とした線形空間への写像と特異値による対角行列によって元の行列を分解することができることを表しています。

さて、単語文書行列を特異値分解で扱う場合に着目すべきは以下の二点です。

自己相関行列である左特異行列、右特異行列が、単語文書行列を対象とした場合に十分な意味合いを持つところ
- 左特異行列は単語 x 単語行列であり、行列の各要素は2索引語の共起頻度を表現する
- 右特異行列は文書 x 文書行列であり、行列の各要素は2文書間における共起語の出現頻度を表現する
主成分分析で固有値が主成分の重みを与えていたのと同様、特異値は U, V を構成する基底の重みを表現している

情報検索アルゴリズムから特異値分解に関する解説で重要な箇所を引用します。

主成分分析と特異値分解は本質的に等価な技術
- 『特異値分解と主成分分析のいずれも、データを表現するための最適な基底として自己相関行列の固有ベクトルを求めているのであり、両者は本質的に等価な技術であるということができる.』(情報検索アルゴリズム P.72)
- 『索引語・文書行列の特異値分解を行うことにより、文書を表現するために最適な正規直交基底と、索引語を表現するために最適な正規直交基底を同時に求めることができる』(情報検索アルゴリズム P.72)

特異値分解は、主成分分析のとき同様、特異値σが次元の重要度を表していて σの小さな次元を無視することで次元を削減できるという性質を持っているだけでなく、分解された左右の自己相関行列が単語文書行列においては語の共起頻度などを"最適な正規直交基底"により表現しているという性質も持っています。任意のドキュメントベクトル d をベクトル積 Ud によって固有ベクトル空間へ写像し、更に重要度の低い基底をσを基準に選んで無視する(すなわち行列の階数を下げる･･･低階数近似。rank(U) = k となるように階数を下げた行列 U_k を考えると d_k = U_kd)ことにより、次元を削減しながら精度を向上することができます。

この次元削減は、単に "car" や "automobile" など特定の単語の次元を削ったのではなく、共起頻度の高い語句を固有ベクトル空間の基底に「縮約」した上で削っているというところが重要です。LSI における、次元を削減しながら "car" で "automobile" がヒットするようになるという性質は、ここから得られます。