HITS, 主成分分析, SVD - naoyaのはてなダイアリー

ウェブグラフのリンク解析によるページの評価と言えば PageRank が著名ですが、もうひとつ Jon Kleinberg による HITS (Hyperlink-induced topic search)も有名です。最初の論文 Authoritative Sources in a Hyperlinked Environment は 1999年です。IIR の 21章で、この PageRank と HITS についての解説がありました。

HITS

HITS はウェブページの評価に二つの軸を用います。一つが authority スコア、もう一つが hub スコアです。

例えば「Perl の情報が欲しい」という検索要求に対しては CPAN や開発者である Larry Wall のホームページなどが重要度の高いページかと思います。これらのページは「Perl に関して信頼できる情報源」ということで、authority (権威的) スコアが高いページです。authority スコアが高いページはたくさんのページからリンクされている、というのは直感的に理解できるでしょう。

一方、Larry Wall のホームページ、CPAN、あるいはオライリーの書籍のページなど、たくさんの authority ページにリンクを張っているまとめサイト的なサイトがあったとしましょう。こちらのページは authority ではないものの、authority ページにたどり着くために有用なページであることから hub (ハブ) と呼ばれ、hub スコアが高いページと言えます。

HITS はウェブグラフのリンク解析によりこの autohrity スコアと hub スコアを計算することで、ページのスコアを算出します。より詳しくは IIR 21章やリンク解析と周辺の話題などが参考になると思います。

反復計算によりスコアベクトルを求める

さて、υ の authority スコアを a(υ), hub スコアを h(υ) とするとそれぞれ

$h(u) \leftarrow \sum_{u \rightarrow y}a(y)$
$a(u) \leftarrow \sum_{y \rightarrow u}h(y)$

と書けます。ページυの hub スコアは、υからリンクしているページ群の authority スコアの和から求まり、authority スコアは υ にリンクしているページの hub スコアの和によって求まるという式です。見て分かる通り、この両者の関係は循環的です。従って、これらのスコアを求めるにはお互いを反復しながら再帰的に計算していくことで最終的な解を求めるという手法を用いることになります。

ここでウェブグラフの隣接関係を行列で表現する隣接行列 A を考えます。A はページ i がページ j にリンクしていたとき A_ij = 1 となる行列です。すると、上式は

$\vec{h} \leftarrow A\vec{a}$
$\vec{a} \leftarrow A^{T}\vec{h}$

と書けます。A を転置した A^T の表現する行列が、リンクの向きでちょうど逆を表しているのが面白いところです。

$\vec{h} = 1$ から始めて $\vec{a}$ と $\vec{h}$ が収束するまで A を掛け続けて、最終的に収束した二本のベクトルがそれぞれ authority スコア、hub スコアのベクトルになります。ページ i の authority スコアは $\vec{a}$ の第i成分となります。hub スコアも同じくです。この手法で欲しいスコアが算出できます。

スコアベクトルは固有ベクトル

ところで上式は相変わらず循環の関係になっていて、 $\vec{h}$ を $\vec{a}$ に、また $\vec{a}$ を $\vec{h}$ にそれぞれ代入すると

$\vec{h} \leftarrow AA^{T}\vec{h}$
$\vec{a} \leftarrow A^{T}A\vec{a}$

となります。さらに ← を = に変えて方程式にするため、係数を導入します。するとなんと

$\lambda\vec{h} = AA^{T}\vec{h}$
$\lambda\vec{a} = A^{T}A\vec{a}$

という式になってしまいました。

求めたかったベクトル $\vec{h}$ や $\vec{a}$ は、AA^T や A^TA で写像しても定数倍になるベクトル、すなわち固有ベクトルであることがこれで分かります。従って、先のように反復計算で収束させる方法以外にも AA^T やA^TA の固有ベクトルを直接算出することでスコアベクトルを得ることもできます。

IIR の 21章によると、反復計算により固有ベクトルを求める方法は PageRank の算出でも使える "べき乗法 (power method)" の計算をしているのと同じ事だそうです。べき乗法で求まるのは主固有ベクトル(一番大きい固有値に対応する固有ベクトル) です。よって、AA^T やA^TA から固有ベクトルを求める場合も主固有ベクトルを考えると両者の解が一致するでしょう。

自己相関行列の主固有ベクトルを求める操作

ここからは自分なりの考察です。

自分自身の転置行列を掛けてその固有値を求めて大きい固有値に対応する固有ベクトルを求める･･･すなわち自己相関行列の主固有ベクトルを求める･･･どこかで聞いたような話だと思ったら、つい先日も言及した　主成分分析や SVD (特異値分解) が全く同じことをしているのでした。同様の話題を扱ったIIR 18章の資料もありますので参照してください。

『特異値分解と主成分分析のいずれも、データを表現するための最適な基底として自己相関行列の固有ベクトルを求めているのであり、両者は本質的に等価な技術であるということができる.』(情報検索アルゴリズム P.72)

HITS もこれと同じだと見なせるのではないでしょうか。

この視点から見ると、HITS の別の側面が見えてきます。主成分分析との比較が分かりやすいでしょう。主成分分析は

基底の変換により主軸を見つける

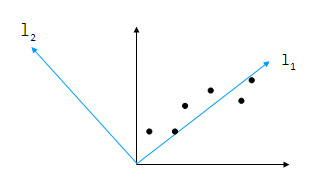
の図のように、データ分布を扱う空間の基底を、より最適な別の基底に変換してから変量を解析する手法です。

主成分分析における「最適な基底」は分散が最大になる方向で、それは共分散行列 (自己相関行列)の固有ベクトルなのでした。上記の図ですと、変換後の l₂ 軸周りにはほとんど情報量がなく、l₁ 軸周りに情報が集中しています。というよりは、そうなるように基底を選ぶのが主成分分析です。l₂ は無視してしまうことで、2次元で扱っていたデータを 1次元で比較、すなわち値の大小関係だけで比較することが可能になります。

HITS も同じように、隣接行列の自己相関行列の主固有ベクトルを選んでいるのですから、同様の操作を行っているとみなすことができそうです。つまり、リンク関係のデータ分布が最も密になるような軸を選んでやって、その軸での値の大小でスコアを決定するということです。これは面白い。

さらに、HITS も PageRank もべき乗法で行列の主固有ベクトルを求めているのですから、PageRank もまた同様のことをやっていると見なせるのではないでしょうか。ということは、PageRank も主成分分析や SVD のように最適な基底を求めて値を比較するなどの操作を全体として行っていると考えられると思いました。SVD に同じく、「次元のたたみこみ」を行っている、ともみなせそう。

こうして考えると HITS や PageRank の直感的イメージが沸いて理解が深まります。